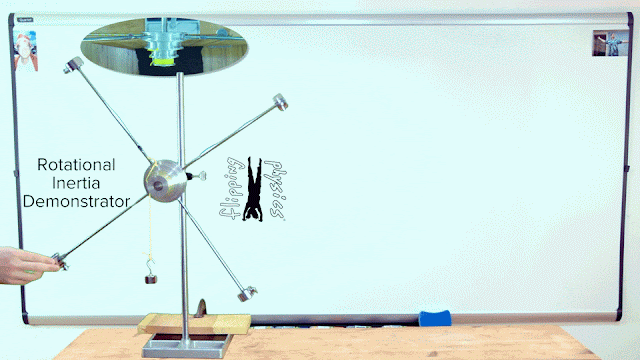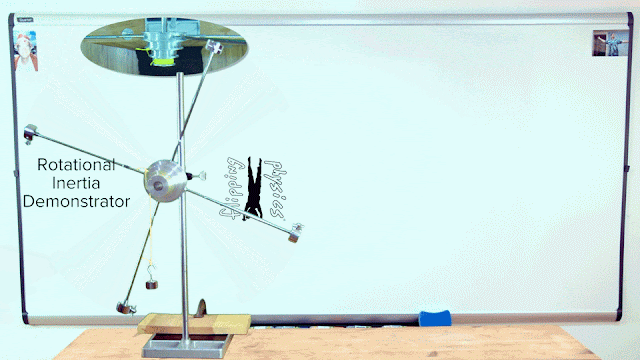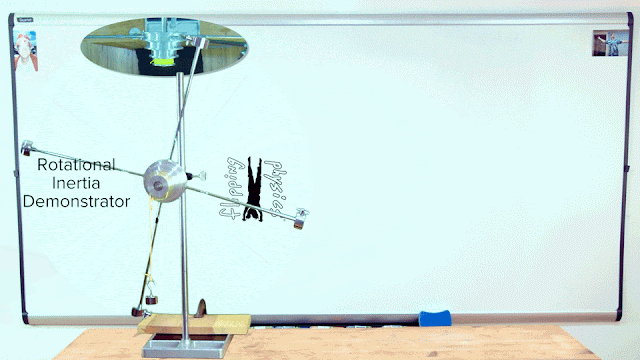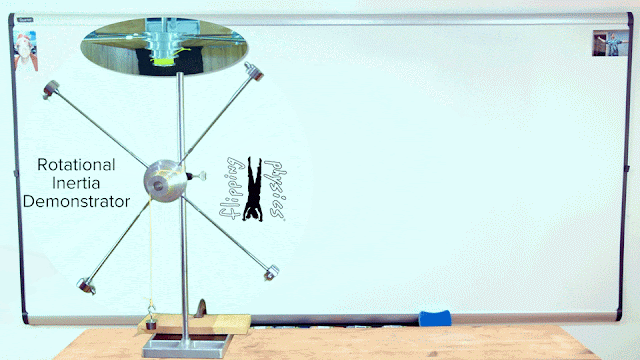
Demonstrating Rotational Inertia (or Moment of Inertia)

Have you ever struggled to describe Rotational Inertia to your students? Even worse, have you ever struggled to understand Rotational Inertia yourself. (I know I have. 😇) Did you know Rotational Inertia is the same as Moment of Inertia? Yeah, I’m with you there. I did not know the name had been changed until recently. However, I do think Rotational Inertia is a more logical phrase than Moment of Inertia. Well, if you would like some help with the concept of Rotational Inertia, then I highly suggest the Rotational Inertia Demonstrator from Arbor Scientific because it is an easy way to demonstrate the concept of rotational inertia. The demonstrator is composed of three pulleys of different sizes all centered around the same axle. Attached to the pulleys are four spokes on which four masses can be placed. The distance from the axle, or axis of rotation, of the four masses on the spokes can be adjusted.

In order to understand rotational inertia, we should first review the equation for rotational inertia of a system of particles:

The rotational inertia of a system of particles equals the sum of the quantity of the mass of each particle times the square of the distance each particle is from the axis of rotation. While the Rotational Inertia Demonstrator does not appear to be a system of particles, the equation for the rotational inertia of a system of particles helps us to understand how the rotational inertia of the demonstrator changes when we adjust the locations of the four adjustable masses. The closer the four adjustable masses are to the axle, or axis of rotation, the smaller the “r” value in the rotational inertia equation and the smaller the rotational inertia of the demonstrator.

...This post is continued on my Flipping Physics page!